Voici cet algorithme appliqué au calcul de  :

1^ère étape :

La première valeur approchée de  est la moitié de 50, c'est à dire 25.

2^e étape :

En divisant 50 par 25, on trouve 2 ; est donc compris entre 2 et 25. La deuxième valeur approchée de  sera la moyenne arithmétique de 2 et de 25 soit 13,5.

3^e étape :

En divisant 50 par 13,5, on trouve 3,7037 ;  est donc compris entre 13, 5 et 3,7037. La troisième valeur approchée de  sera la moyenne arithmétique de 13,5 et de 3,7037 soit 8,6018.

Étapes suivantes :

On continue autant de fois qu'il est nécessaire en répétant le procédé. Nous accepterons, sans le démontrer, qu'on obtient ainsi des valeurs approchées de plus en plus précises de .

La méthode se généralise à tout nombre positif.

Au lieu d'utiliser le langage courant pour décrire un algorithme, on peut utiliser un organigramme qui le présente de manière plus visuelle et surtout plus synthétique.

Les organigrammes, très à la mode au début de l'informatique, sont aujourd'hui moins utilisés. Mais dans certains cas, ils sont extrêmement utiles à la compréhension.
 

Avant de présenter l'organigramme, nous ferons trois remarques qui permettront de mieux comprendre comment il a été construit. 

1°) On peut observer que, la première approximation mise à part, toutes les autres sont calculées de la même façon. : si v est l'approximation qui suit immédiatement l'approximation u, on a v=.
Le même calcul est donc répété un certain nombre de fois.

2°) Contrairement à ce qu'on pouvait penser à priori, la formule  v= montre que deux variables seulement suffisent pour décrire la suite des valeurs approchées de . 

3°) Il existe différents moyens d'arrêter les calculs. On peut fixer à l'avance le nombre des approximations qui seront calculées, 20 ou 30 par exemple. On peut aussi décider de stopper les calculs lorsque une certaine précision, fixée elle aussi à l'avance, est atteinte. Pour cela, au cours des calculs, on peut tester la valeur absolue de la différence de deux valeurs approchées consécutives uet v. On décidera par exemple de cesser les calculs dès qu'on aura < 10^-6.

Voici maintenant l'organigramme annoncé :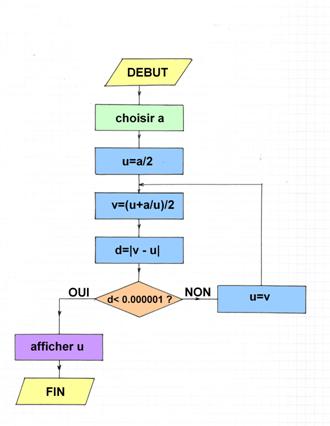

Cet organigramme a un début et une fin. Il comprend 3 variables numériques (u, v et d) ainsi qu'une constante numérique (c'est a). Les instructions qu'il comporte sont exécutées une à une, de manière séquentielle. Une « boucle » répète le même calcul tant que c'est nécessaire mais naturellement avec des valeurs différentes. Le nombre de répétitions dépend du résultat du testd>0,000001 placé dans la case rose. Selon la réponse à ce test, les calculs sont poursuivis ou stoppés. 

L'organigramme comporte plusieurs types d'instructions. On trouve en particulier :

- une instruction d’entrée (case verte) : on choisit de calculer non pas seulement  mais la racine carrée d'un nombre a quelconque mais positif ; comme la valeur de a ne change jamais dans la suite des calculs, on dit que c'est une constante numérique ;

- des instructions d'affectation (cases bleues), représentées par le signe = ;

- une instruction de sortie (case violette) ;

- une instruction conditionnelle (case rose).

L'organigramme qui schématise l'algorithme de Babylone peut être transcrit presque immédiatement dans un langage de programmation. Avec le langage de programmation PYTHON, on obtient le programme suivant  :

a=input("Choisir a :" )

u=a/2.0

d=abs(a-u)

while d>0.000001 :

    v=(u+a/u)/2.0

    d=abs(u-v)

    u=v

print u

Même si les instructions sont exprimées en anglais, on reconnaît la démarche utilisée dans l'organigramme.

L'entrée du nombre a se fait à l'aide de l'instruction input() : c'est un mot anglais d'origine latine qui signifie « introduire, mettre dedans ».

Le mot-clé anglais while, qui signifie tant que..., sert à définir une boucle conditionnelle.

La précision demandée est atteinte lors du calcul de la 7^e valeur approchée. Celle-ci vaut  7,07106781187.

Un programme est donc la mise en œuvre d'un ou de plusieurs algorithmes, dans le cadre d'un langage de programmation.