SOLUTION
On applique le théorème de Pythagore au triangle rectangle de la figure :
65 = (81 ‒ 16)2 = (81 – l / 2)2 + (L / 2 – 16)2.
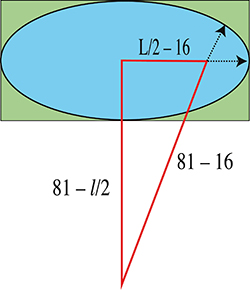
Ni l, ni L ne peuvent êtres impairs ; on a donc affaire à des nombres entiers appartenant à des triplets pythagoriciens de la forme suivante :
On supposera que est supérieur à
et qu’ils sont premiers entre eux. Il existe alors un entier
tel que
(ou bien l’inverse).
On a alors les possibilités suivantes.
= 1,
= 8 et
= 1 donne 81 – l / 2 = 63 et L / 2 – 16 = 16 (ou bien l’inverse).
= 1,
= 7 et
= 4 conduit à 81 – l / 2 = 33 et L / 2 – 16 = 56 (ou bien l’inverse).
= 5,
= 3 et
= 2 fournit 81 – l / 2 = 25 et L / 2 – 16 = 60 (ou bien l’inverse).
= 13,
= 2 et
= 1 aboutit à 81 – l / 2 = 39 et L / 2 – 16 = 52 (ou bien l’inverse).
On obtient ainsi huit solutions : (l ; L) = (36 ; 64), (130 ; 158), (96 ; 144), (50 ; 98), (112 ; 152), (42 ; 82), (84 ; 136) ou (58 ; 110).

