Paul Erdős s’est intéressé aux produits de nombres entiers consécutifs. Dans une note datant de 1939 publiée dans The Journal of The London Mathematical Society, il démontre que le produit d’au moins deux nombres entiers consécutifs strictement positifs n’est jamais un carré. Il cite également ce qui n’est alors qu’une conjecture : un tel produit n’est jamais une puissance d’un entier d’exposant strictement plus grand que 1. Il démontrera cette conjecture dans un article publié en 1975 avec le mathématicien américain John Lewis Selfridge (1927-2010).
Les quadriges
Appelons quadrige un nombre égal au produit de quatre entiers naturels consécutifs non nuls, augmenté de 1.
Par exemple, 5 × 6 × 7 × 8 + 1 = 1681 est un quadrige.
On observe que 1681 est le carré d’un nombre entier : 1681 = 412.
1. Démontrez que tout quadrige est le carré d’un nombre entier.
On pourra éventuellement s’aider de la preuve sans mot représentée ci-dessous.
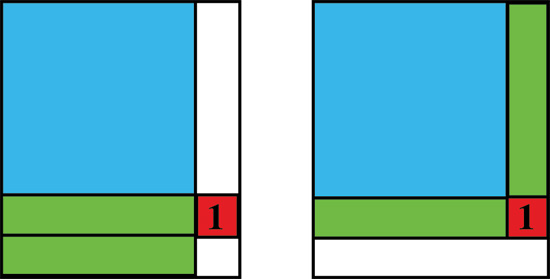
Si un quadrige est toujours un carré, on peut en déduire que le produit de quatre nombres entiers consécutifs non nuls n’est jamais le carré d’un nombre entier. En effet, à l’exception de 0 et 1, la différence entre deux carrés d’entiers consécutifs est toujours strictement supérieure à 1. On retrouve le résultat d’Erdős dans le cas particulier de quatre entiers consécutifs strictement positifs.
Produits de quadriges
D’autres questions amusantes peuvent être posées à propos des quadriges.
Le produit de deux quadriges ou de trois quadriges peut-il être un quadrige ?
La réponse est positive.
Désignons par Q(n) le quadrige n(n + 1) (n + 2) (n + 3) + 1.
|
n |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
Q(n) |
25 |
121 |
361 |
841 |
1681 |
3025 |
5041 |
7921 |
11881 |
17161 |
On observe que Q(1) × Q(2) = Q(6).
Par ailleurs, Q(5) × Q(6) = 1681 × 3025 = 5 085 025 = 25 × 3 × 72 × 23 × 47 + 1
= 46 × 47 × 48 × 49 + 1 = Q(46).
On a donc Q(5) × Q(1) × Q(2) = Q(46).
Mais il y a plus simple :
Q(2)3 = 1213 = 1 771561 = 23 × 32 × 5 × 7 × 19 × 37 + 1 = 35 × 36 × 37 × 38 + 1 = Q(35).
On observe aussi que Q(2) = 1 × 3 × 5 × 7 + 24 = 121
et Q(3) = 1 × 4 × 7 × 10 + 34 = 361.
2. Montrez que pour tout n ≥ 1, Q(n) = 1 × (1 + n)(1 + 2n)(1 + 3n) + n4.
Une dernière remarque :
Q(1) + Q(2) + Q(3) = 25 + 121 + 361 = 507 = 3 × 132.
3. Montrez que la somme de trois quadriges consécutifs est toujours égale au triple du carré d’un entier.

